Batch 2 - Class 76 - Mathematical Hockey
Attendance: Anisha, Smiti, Muskaan, Tishyaa, Adit, Diya, Nandini, Liza
Class Notes:
Explain the rules of Mathematical Hockey
- Two teams; each player must take turns - can do random or assigned play as long as everyone gets turn
- 5 minutes per problem. Person to answer first wins if answer is right. Else the other person wins without having to answer
- If no one answers for 5 minutes, then 30 seconds for the next person scheduled on the team to answer
- Draw the hockey rink and goal posts and zones
- Display problems on TV screen
- For Auction Problems, each team bids for a problem, and the winning team gives the bid amount to Instructor. The winning team gets to present an answer. After that the bid continues for better answers. Finally, the best answer after all bids wins all the amount with the Instructor. Amount can be used as goal steps.
Individual Puzzles:
- What fraction of this square region is shaded? Stripes are equal in width, and the figure is drawn to scale.
- Answer: 7/12 (Divide the big square into 36 smaller squares)
- Fourteen white cubes are put together to form the figure below. The complete surface of the figure, including the bottom, is painted red. The figure is then separated into individual cubes. How many of the individual cubes have exactly four red faces?
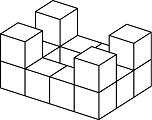
- Answer: 6 (these are cubes which have two hidden sides)
- The digits 0-9 can be rearranged into 3628800 distinct 10 digit numbers. How many of these are prime?
- Answer: None (the sum of digits is 45, so all numbers are divisible by 3)
- Complete the square logically

- Answer: Upside down club is always to left of right side up heart
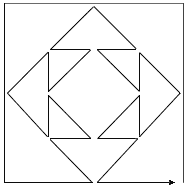
- How is it possible to trace this design in one continuous movement without crossing a line on the way?
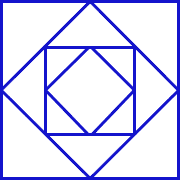
- Answer:
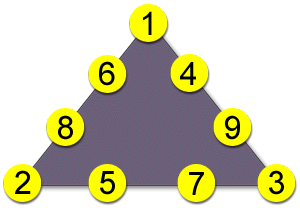
- Place the numbers 1 through 9 in the circles below, such that each side of the triangle adds up to 17
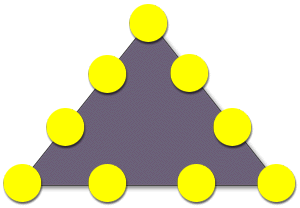
- Answer:
Math Auction Style Problems:
- Place as many rooks as you can on a chess board so that each rook attacks an odd number of other rooks
- Best answer obtained: 24 Rooks
- Using the number 8 and the operations of addition, subtraction, multiplication, division, and exponentiation (and parentheses), write a mathematical equation that evaluates to 100. What is the smallest number of 8's that you can use?
- Best answer obtained: (888-88)/8
- A wooden stick is to be made into a ruler by marking it with labels. Your goal is to be able to measure any integer distance between 1cm and 20 cm (including 1cm and 20cm) without moving the ruler. That is to say, for any number 1 ≤N≤20, there should be two tick marks on the ruler that are Ncm apart. What is the smallest number of tick marks you can use?
- Best answer obtained: 8 Markers
- A tower of 80 coins is placed at the central square of a 1 × 1001 board. During a turn, one can lift k of top coins from any tower (you can lift any number of coins, even all coins), and place them onto a square k fields to the right or to the left. If this square contains some coins already, then the relocated coins are placed on top. The goal is to relocate all coins from the original position to the square immediately right from it. Do this in as few turns as possible.
- Best answer obtained: 14 turns
Team Game:
- Use all 12 pentonimoes to make a rectangle (any size: 10x6, 20x3, 15x4 or 12x5) - 5 minutes, team game - each team gets points for each solution they can come up with
- Answer:
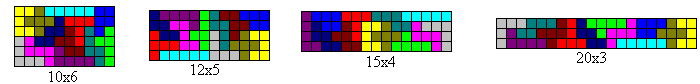
- 3D Tic-tac-toe Competition (Each team member to each) - Download the 3D Tic-tac-toe game on your phone/online (https://www.mathsisfun.com/games/foursight-3d-tic-tac-toe.html) - Note that this is a 4x4x4 tic tac toe game.
Homework
- Arrange numbers 1-32 in a circle so that any two adjacent numbers sum to a square
- Answer:
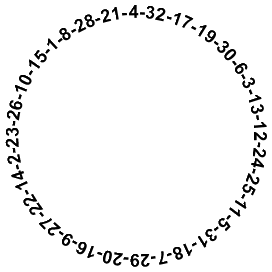
References: